Specializace: Finanční a pojistná matematika

Tato specializace je určena studentům, kteří se chtějí uplatnit ve finančním a pojistném sektoru jako analytici dat, odborníci na finanční deriváty a portfolia, analýzu rizik, data mining a pojištění. Samozřejmě se tím myslí odborné pozice v centrálách bank, finančních či pojistných institucí, či velkých firem na finančním trhu.

Stochastické procesy ve finanční matematice

Stochastické procesy dávají velmi účinný nástroj pro modelování nejrůznějších reálných dějů. Tento kurz se soustředí na procesy, které hrají klíčovou roli ve finanční a pojistné matematice. Věnuje se vlastnostem náhodné procházky, Wienerova procesu, Poissonova procesu a příkladům jejich využití. Předmět poskytuje matematický základ pro aplikace v modelech finanční a pojistné matematiky využívaných v praxi.

Oceňování finančních derivátů

V tomto předmětu se naučíte oceňovat opce a další finanční deriváty a řešit praktické úlohy spojené s jejich použitím. Oceňovací teorie spojuje elegantní a sofistikované matematické modely a aplikace teorie pravděpodobnosti s reálnými problémy finanční matematiky.

Matematické modely ve financích

V tomto kurzu se dozvíte, jak pojišťovny a jiné finanční instituce vytvářejí své oceňovací modely, jak využívají GLM modely nebo „machine learning“ techniky i jak určují výši bonusů nebo malusů svým klientům. Přednášky jsou doplněny praktickými příklady za použití softwaru R.

Analýza přežití

V tomto předmětu se dozvíte aplikace teorie maximální věrohodnosti v modelech pro výskyt událostí v čase nebo pro (ne)podmíněné riziko sledované události, metody odhadu konkurujících si rizik, funkce přežití, jejích intervalů spolehlivosti, teorii Coxova regresního modelu proporcionálních rizik i simulační studie v softwaru R včetně aplikace metod na reálná data.

Specializace: Statistika a analýza dat

Tato specializace je určena studentům, kteří se chtějí uplatnit v široké oblasti statistické analýzy dat. Nalézt uplatnění je možné v mnoha institucích, od zpracování laboratorních, medicínských či vědeckých dat až po oblast komerční sféry.

Pokročilé regresní modely

Obyčejnou metodu nejmenších čtverců zná každý absolvent bakalářského programu. Dá se s ní dojít daleko, ale znalost pokročilejších regresních metod lze použít například pro extrapolaci mimo rozsah dat nebo pro regresní analýzu korelovaných a cenzorovaných dat. Tento předmět se zaměřuje na vybrané moderní regresní metody, které se používají v prediktivních a konfidenčních analýzách ve statistické datové vědě a ve výzkumu.

Statistická inference

Otestovat korektně nulovou hypotézu není zdaleka tak jednoduché, jak by se mohlo zdát a ne na každý interval spolehlivosti je opravdu spolehnutí. Statistické testy spolu neustále soupeří v síle a vyhrává ten nejsilnější. Jak ho ale mezi ostatními najít? To a mnoho dalšího nabízí kurz statistické inference spolu s programováním uvedených metod, funkcí, grafů i animací v softwaru R.

Teorie pravděpodobnosti

Teoretický předmět vysvětluje, jak se konstruuje pravděpodobnostní prostor, co skutečně je hustota pravděpodobnosti, proč máme pro náhodné veličiny více konvergencí, jak funguje rozšíření pravděpodobnosti z konečně mnoha na nekonečně mnoho opakování, i jak konstruovat jiná než diskrétní a spojitá rozdělení pravděpodobnosti.

Bayesovské metody

Předmět vykládá principy bayesovské statistiky pro správné použití v praxi, např. pro modelování prevalence chorob, počtu dětí matek, délky spánku studentů nebo pro zkoumání závislosti množství vstřebaného kyslíku při cvičení v závislosti na věku. K tomu je třeba rozlišit apriorní a aposteriorní rozdělení pravděpodobnosti, znát Metropolisův algoritmus a Gibbsův vzorkovač.

Specializace: Modelování a výpočty

Tato specializace je určena studentům, kteří se chtějí uplatnit v modelování a simulacích reálných dějů, jak stochastických, tak deterministických. Uplatnění je možné nalézt v širokém spektru oblastí od medicíny, neurovědy, ekologie či epidemiologie až po makroekonomii či matematiku samotnou, jejíž vědecká oblast numerické matematiky se stále rozvíjí.

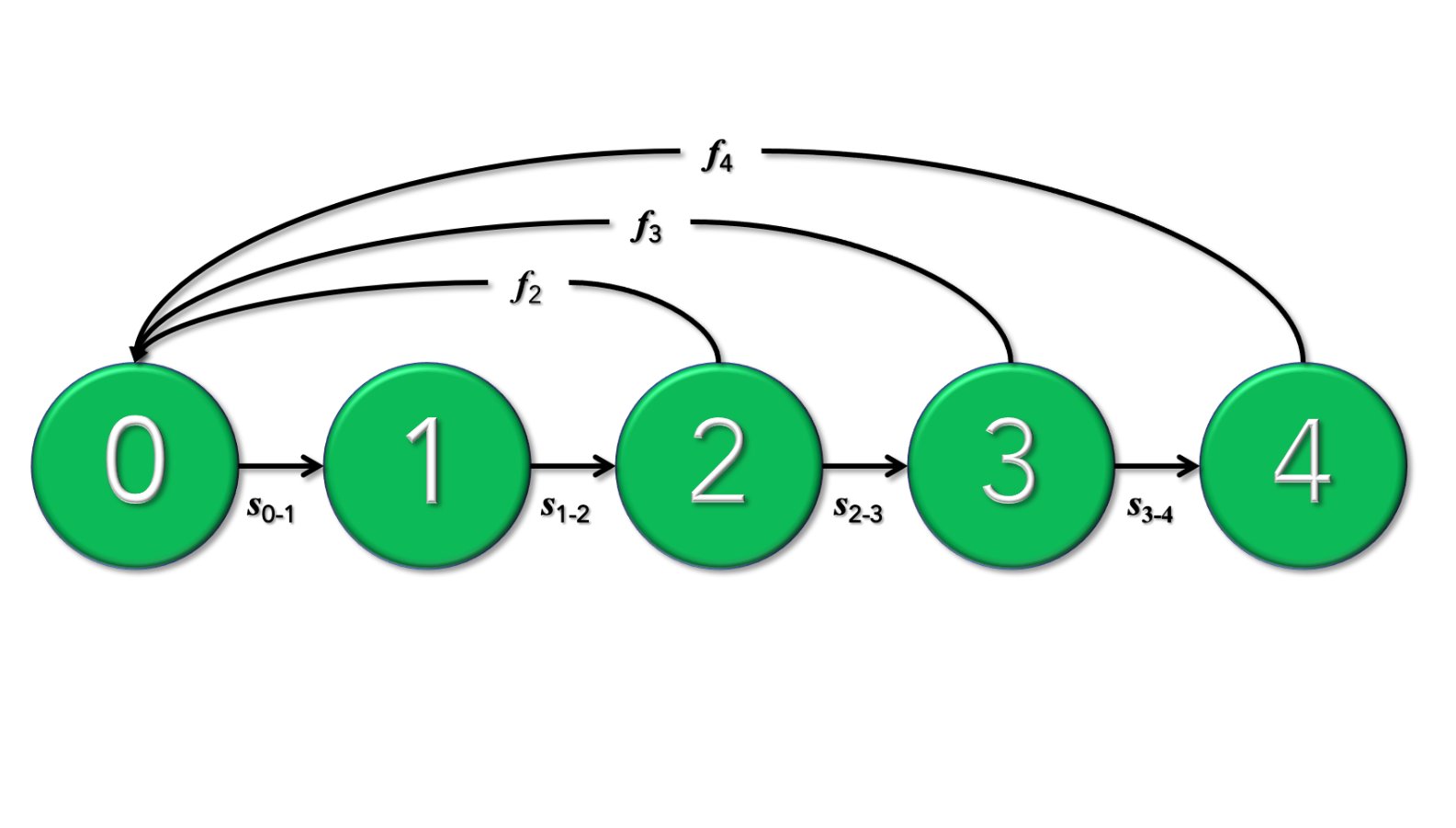
Strukturované populační modely

Fibonacciovy králíky, Leslieho krysy i bodláky na kraji lesa lze popsat stejným matematickým populačním modelem. Avšak slovo „populace“ označuje jakýkoliv soubor abstraktních objektů. Při konstrukci, analýze a interpretaci takového modelu se potkávají teorie diferenčních rovnic, lineární algebra, teorie grafů, statistika, regresní analýza i teorie náhodných procesů. Tyto disciplíny společně nabízejí odpovědi na důležité otázky při ochraně přírody nebo ochraně lidských zájmů, ale i na důležité existenciální otázky života.

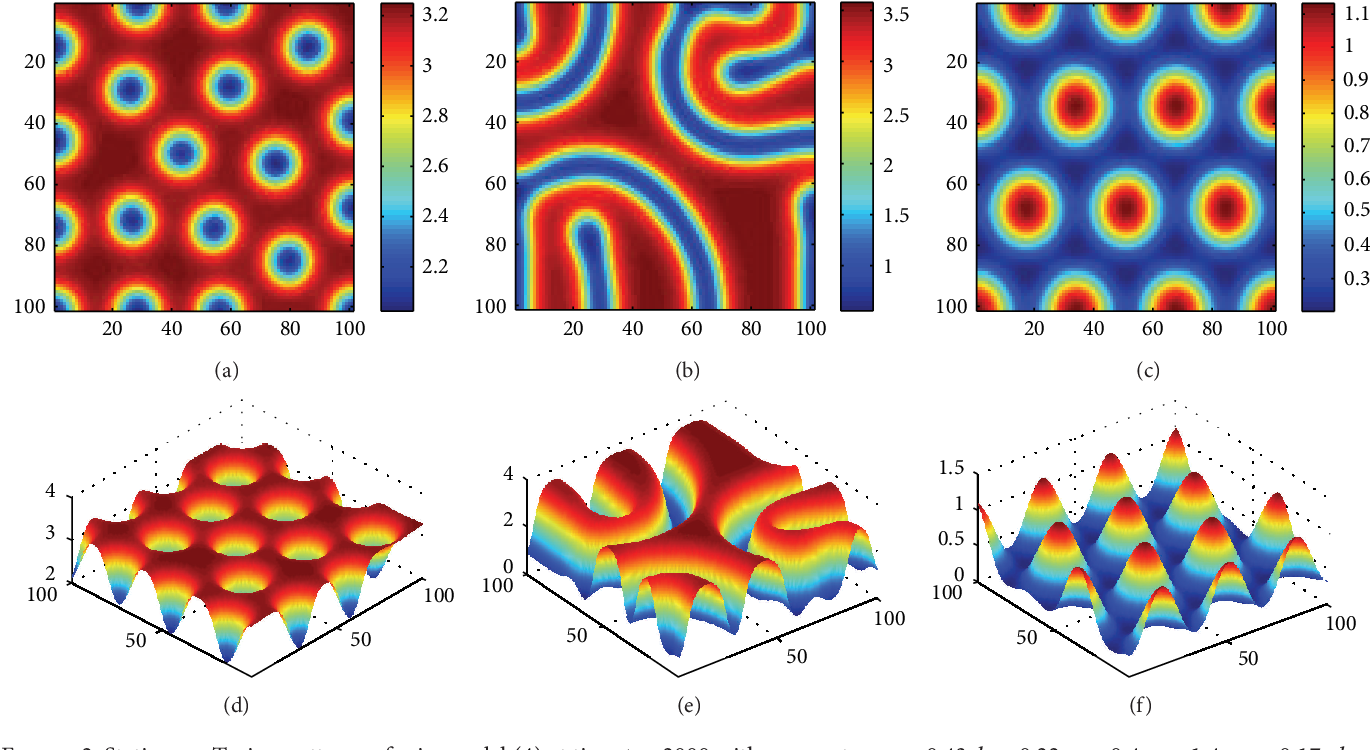
Spojité deterministické modely II

Předmět navazuje na bakalářský, který se věnuje modelům pomocí obyčejných diferenciálních rovnic, které lze použít např. pro modelování vývoje velikosti populace a jejích interakcí, šíření různých typů epidemie nebo makroekonomických modelů. Pro modely, kde nejsou všichni jedinci v populaci stejní, nebo když je populace nerovnoměrně rozptýlená v prostoru je třeba použít aparát parciálních a funkcionálně diferenciálních rovnic vyučovaný v tomto kurzu.

Teorie bifurkací, chaos a fraktály

Teoretický předmět doplňující bakalářský Nelineární dynamika a její aplikace. Umožňuje porozumět chování dynamických systémů, kvalitativním změnám dynamiky a principům, které za těmito složitými jevy stojí. Aplikace lze nalézt v medicíně, biochemii, neurovědě, hydrodynamice, astrofyzice, ekonomii, ekologii, evoluční biologii a v mnoha dalších oblastech vědy.

Stochastické modely markovského typu

Předmět se věnuje stochatickým modelům markovského typu s využitím simulací. Základní pojmy teorie hromadné obsluhy jsou doplněny optimalizačními úlohami v systémech hromadné obsluhy i analýzou Galtonova—Watsonova procesu větvení pomocí pravděpodobnostní vytvořující funkce.

Specializace: Diferenciální rovnice a jejich aplikace

Parciální diferenciální rovnice

Předmět se věnuje hlavním výsledkům teorie parciálních diferenciálních rovnic (tedy látce stručně označované jako "PDE"). Důraz je kladen na čtyři (v aplikacích fundamentální) rovnice, a to lineární transportní rovnici, Poissonovu (Laplaceovu) rovnici, rovnici vedení tepla a vlnovou rovnici. V předmětu nechybí základní metody řešení PDE, jako jsou metoda charakteristik pro rovnice 1. řádu, metoda separace proměnných či Fourierova transformace. Z čistě teoretické látky je pak největší pozornost věnována Cauchyově—Kovalevské větě.

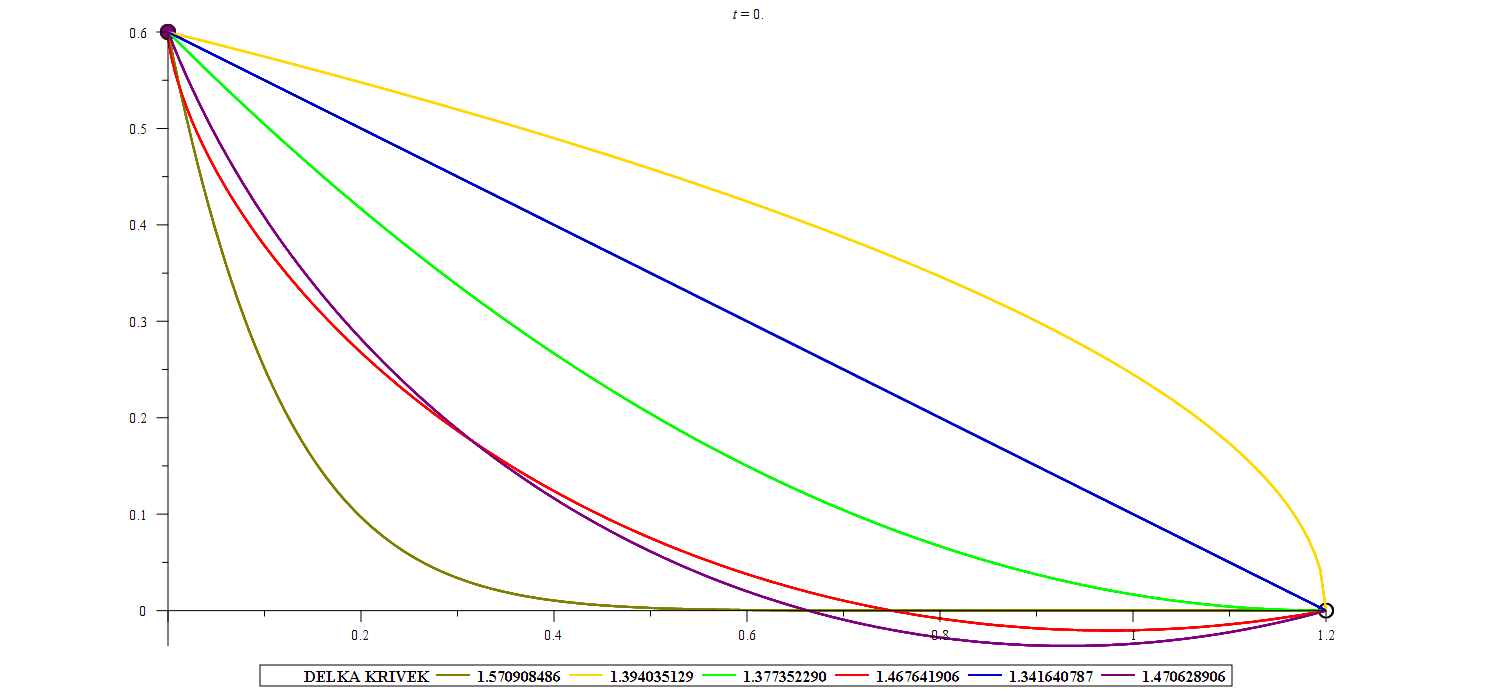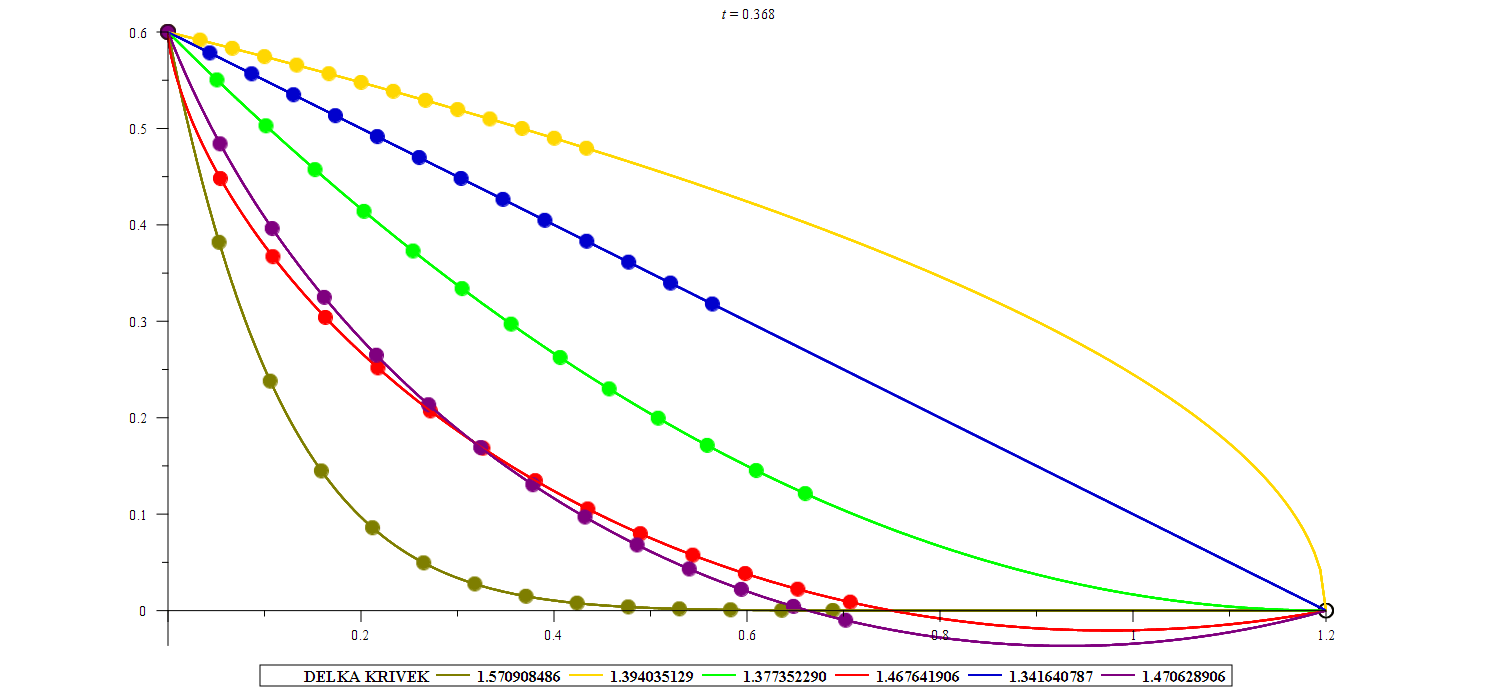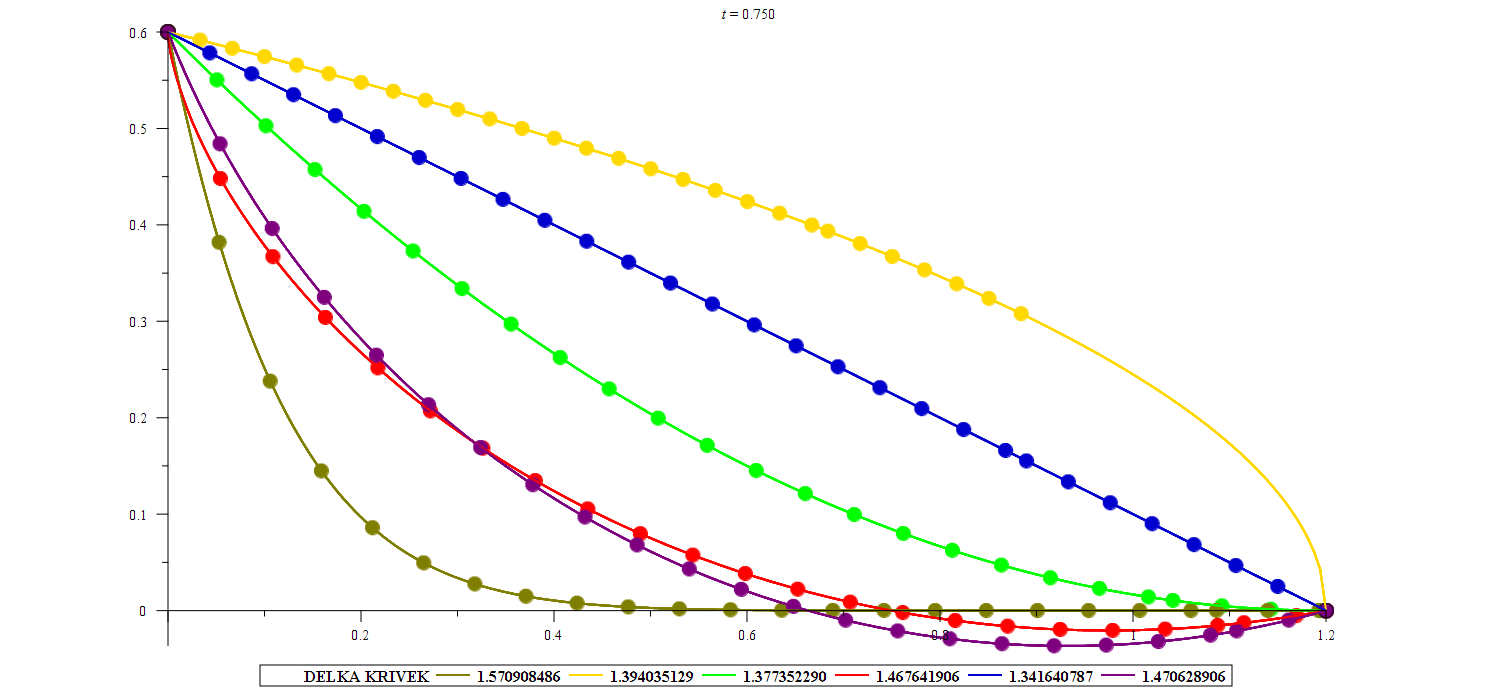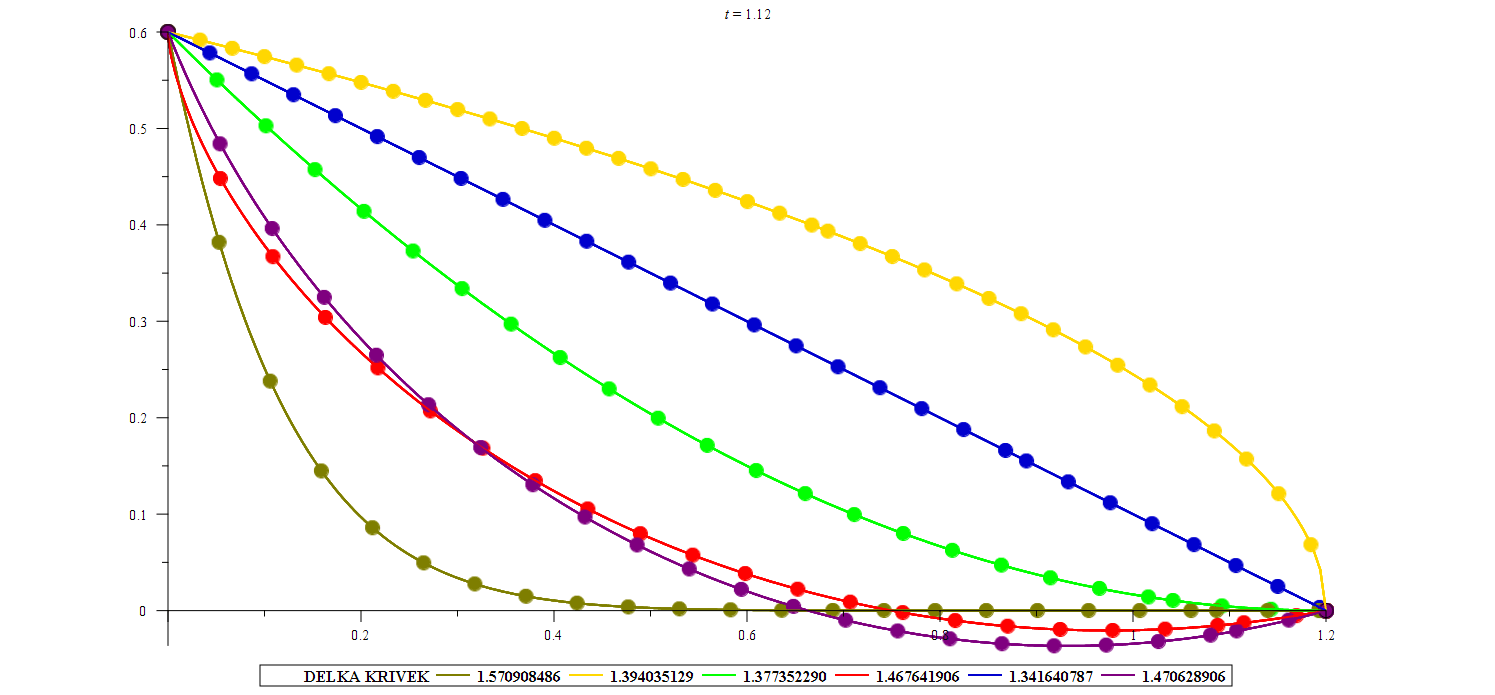
Variační počet

Předmět se věnuje studiu extrémů funkcionálů, což jsou zobrazení z množiny funkcí do reálných čísel. Typickými příklady funkcionálů jsou určité integrály na množině vhodných funkcí. Tyto funkcionály mohou popisovat důležité procesy v přírodě, např. vzdálenost dvou míst na zadané ploše (např. na Zemi), čas nebo energii potřebnou k cestování mezi dvěma body v prostoru, plochu uzavřenou křivkou zadané délky, povrch rotačního tělesa zadaného funkcí. U všech těchto úloh nás zajímá, jestli lze daný proces realizovat optimálně, tj. s minimální vzdáleností, s minimálním časem nebo minimální energií, s maximální uzavřenou plochou, atd. Řešením takové úlohy je pak funkce – extremála. Tyto úlohy se řeší pomocí diferenciálních rovnic. Historie tématu sahá až do konce 17. století, kdy byla formulována úloha o brachistochroně – křivce, po které se lze pohybovat s minimálním časem. Znalosti z tohoto předmětu tedy umožňují řešit různé reálné optimalizační úlohy a jsou vhodným rozšířením základních principů pro hledání extrémů funkce jedné nebo více proměnných.

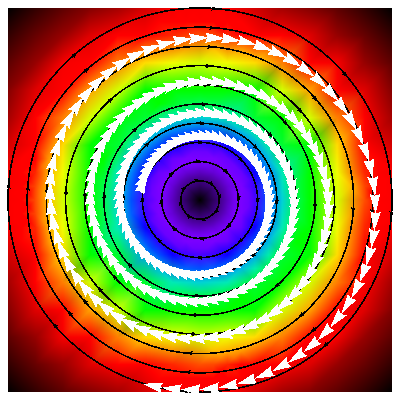
Diferenční rovnice

S rozvojem infinitesimálního počtu na konci 17. století je úzce propojené také prohloubení výsledků z oblasti diferenciálních rovnic, které se využívají především při modelování různých fyzikálních jevů. Avšak ne vše kolem nás probíhá ve „spojitém“ čase, např. úroky v bance se počítají na pouze základě celočíselného počtu dní a menší části se již nezohledňují. Pro modelování takovýchto situací jsou mnohem vhodnější diferenční rovnice, kterým je věnován právě tento předmět. Kurz je doplněn o úvod do diferenčního a sumačního počtu, ve kterém jsou mj. zdůrazněny hlavní odlišnosti od infinitesimálního počtu.