Tento program má 4 specializace: obecná matematika, finanční a pojistná matematika, statistika a analýza dat a modelování a výpočty. Zvlášť po absolventech aplikované matematiky je aktuálně vysoká poptávka ve firmách a institucích poptávajících analýzu dat. Na specializaci obecná matematika navazuje magisterský studijní program Matematika. Pro ostatní specializace má přímou návaznost magisterský program Aplikovaná matematika, který má opět čtyři možné specializace (tři se shodným názvem jako v bakalářském programu plus jednu novou). Směr studia není neměnný — při pokračování v magisterském programu je možné zvolit jinou specializace než v bakalářském (včetně volby jiného magisterského programu než toho, který odpovídá specializaci v bakalářském programu).

Více informací včetně přihlášky najdete zde.

Společné předměty programu Matematika

Během studia se studenti setkají s předměty z matematické analýzy, algebry, statistiky, informatiky a dalších oblastí. V navazujícím magisterském programu je sice výhodné pokračovat ve zvolené specializaci, ale je možné volit i jinou.

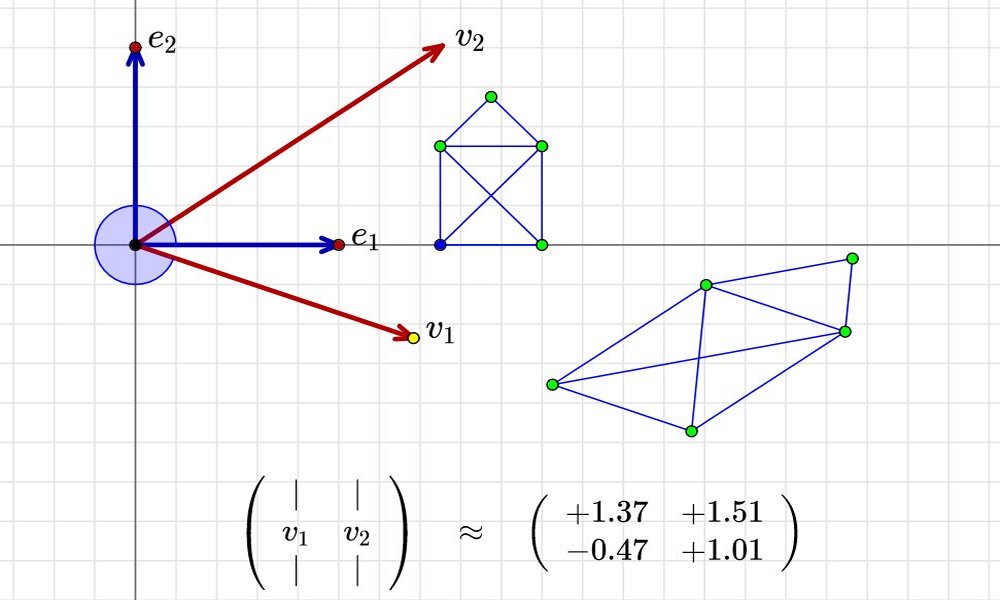
Lineární algebra

Jedna z nejdůležitějších oblastí matematiky, jejíž aplikace se prolínají všemi oblastmi matematiky. Teoretický předmět, kterým musí projít každý absolvent programu. Lineární vektorové prostory jsou totiž všude – a i tam, kde nejsou, je vhodné si je aspoň vhodně vytvořit a definovat.

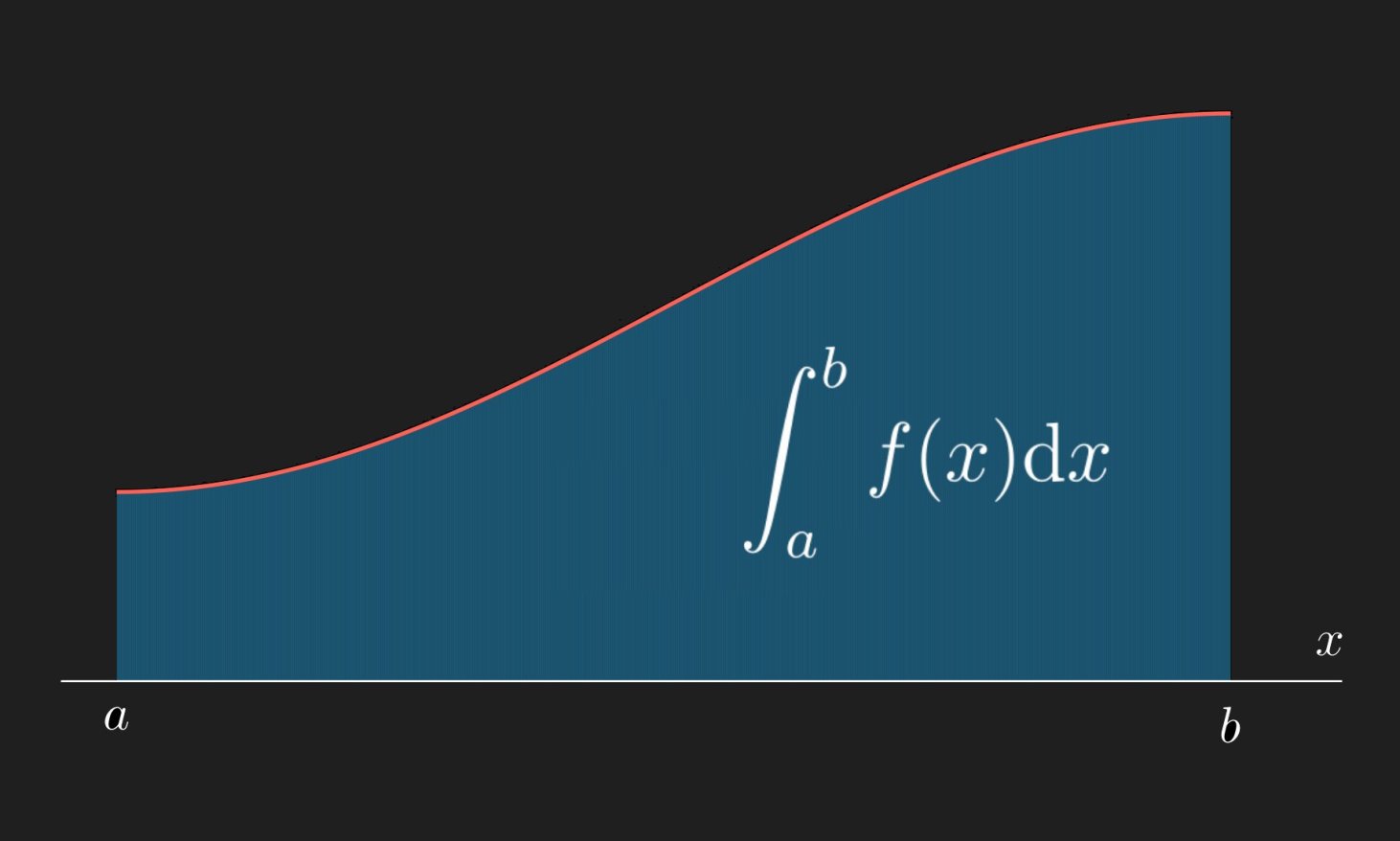
Matematická analýza

Další teoretický předmět programu, protože ani v obecné matematice, ani v aplikované matematice se neobejdete bez diferenciálního a integrálního počtu. Je základem např. optimalizačních metod využívaných v numerické matematice nebo finanční sféře, stejně tak je významná pro modelování i statistiku.

Pravděpodobnost a statistika

Tento předmět (ve dvou semestrech) pokrývá základy teorie pravděpodobnosti a nejdůležitější statistické metody. Významné teoretické i aplikované výsledky stojí právě na nich.

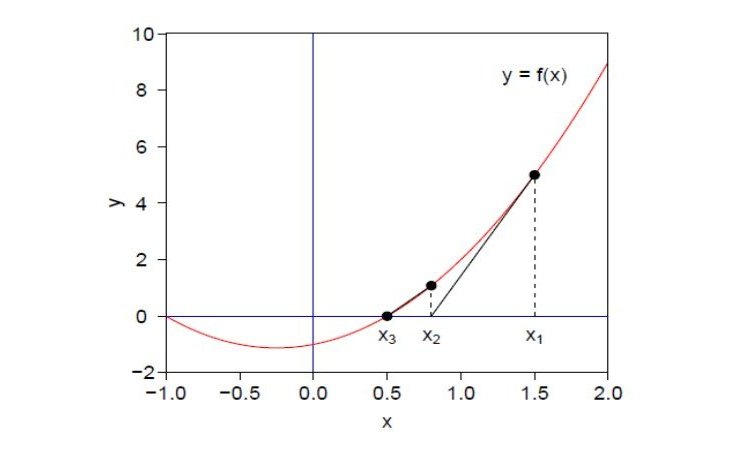
Numerické metody

Často se stane, že matematický model nebo rovnici nejde jen tak vyřešit. Pak pomáhají numerické metody. Ty slouží nalezení řešení mnoha úloh, které je složité nebo dokonce nemožné jinak vyřešit. Algoritmy je třeba nejen pochopit, ale také implementovat na počítači!

Specializace: Obecná matematika

Specializace Obecná matematika je vhodná pro všechny studenty s netriviálním zájmem o matematiku. Jde o specializaci, u které se nepředpokládá, že student ví, jaké partii matematiky se chce primárně věnovat. Cílem této specializace je kvalitní obecný přehled absolventa. Není tedy vhodná pro ty, kteří se chtějí cíleně soustředit kupř. na finanční matematiku. Rozsah předmětů tak není nijak specificky zúžen a studenti mají v rámci povinných předmětů základní kurzy matematické analýzy, lineární algebry, algebry, pravděpodobnosti a statistiky, numerické a finanční matematiky doplněné o vhodné navazující předměty, které umožňují získat ucelený přehled o vysokoškolské matematice. Na bakalářské studium lze pochopitelně (nejen u nás) navázat studiem magisterským (kde se poté rovněž nabízí možnost cíleně se soustředit na zvolenou oblast), popřípadě studiem doktorským.

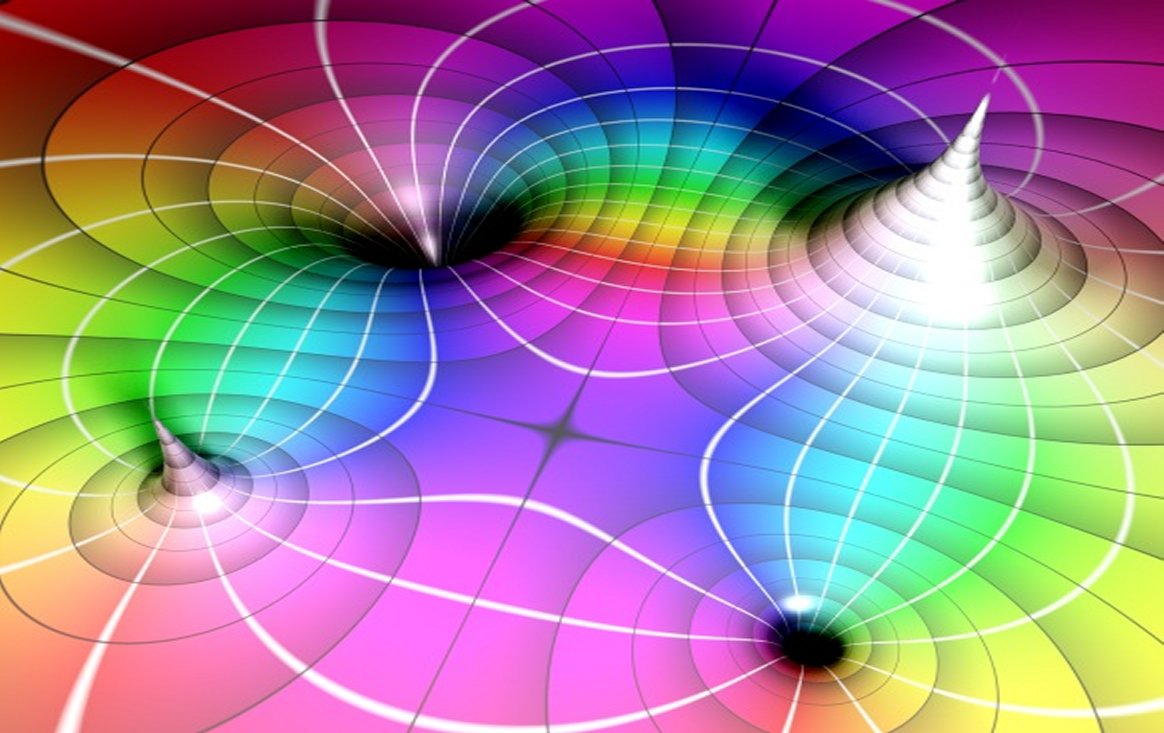
Analýza v komplexním oboru

Tato klasická partie matematické analýzy má různé elegantní a mnohdy i nečekané aplikace v mnoha oblastech matematiky. Je účinným nástrojem i mimo matematiku, hlavně ve fyzice a technice. Cílem kurzu je seznámit studenty se základy teorie funkcí komplexní proměnné, zejména s integrací v komplexním oboru a Cauchyovou teorií, vlastnostmi holomorfních funkcí, teorií reziduí a jejími aplikacemi.

Funkcionální analýza

Tento teoretický předmět patří mezi základní univerzitní kurzy matematiky. Je využívána v řadě dalších předmětů i v mnoha aplikacích. Cílem předmětu je seznámit posluchače se základními pojmy lineární funkcionální analýzy, zejména s lineárními prostory, jejich duálními (adjungovanými) prostory a s lineárními funkcionály.

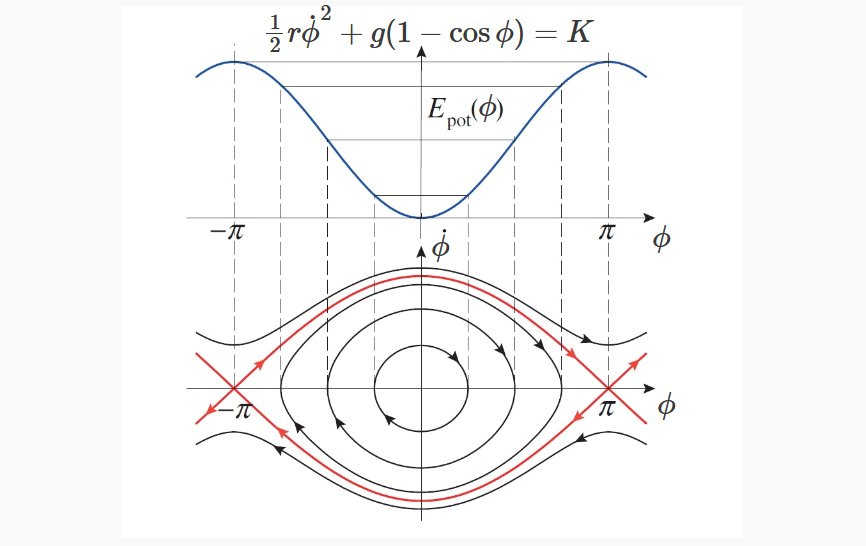
Obyčejné diferenciální rovnice

Teorie diferenciálních rovnic patří mezi základní oblasti matematické analýzy. Je využívána v řadě dalších předmětů i v mnoha aplikacích. Základním cílem kurzu je seznámit studenty se základy teorie obyčejných diferenciálních rovnic, vybranými partiemi teorie stability a kvalitativní teorie diferenciálních rovnic a ukázat souvislosti s jinými oblastmi matematiky.

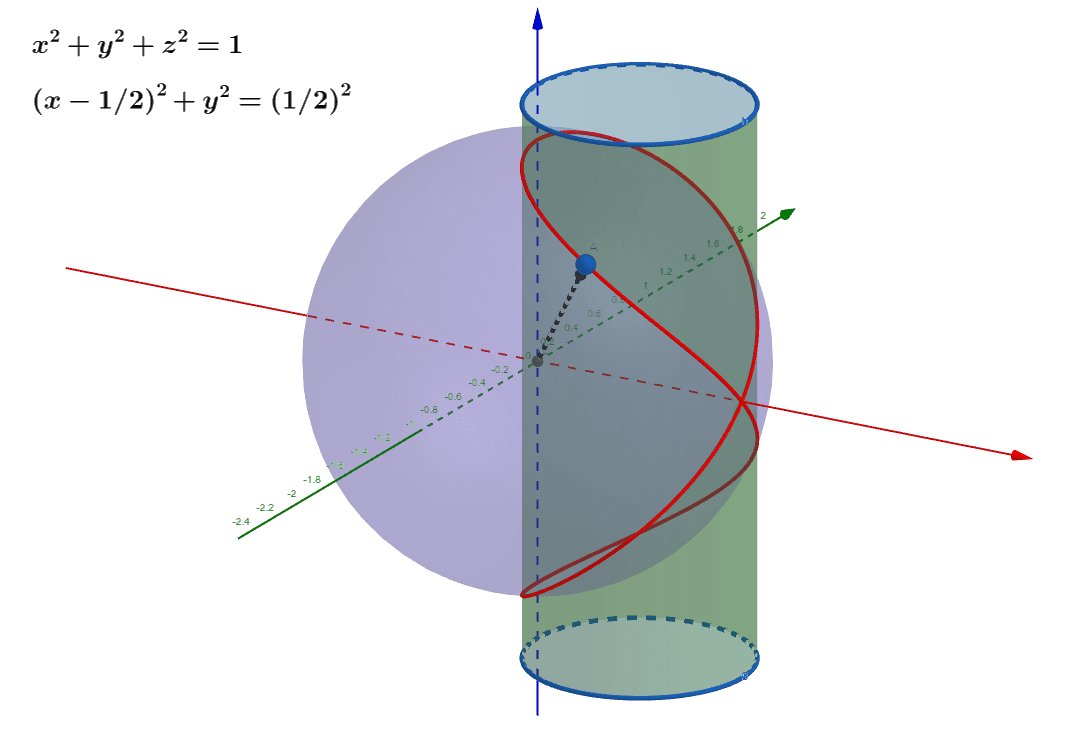
Diferenciální geometrie křivek a ploch

Kurz obsahuje ucelený přehled hlavních ideí a výsledků diferenciální geometrie křivek a ploch v trojrozměrném euklidovském prostoru. Toto zahrnuje jak teorii lokálních invariantů, tak globální vlastnosti křivek a ploch.

Specializace: Finanční a pojistná matematika

Tato specializace je určena studentům, kteří se chtějí uplatnit ve finančním a pojistném sektoru jako analytici dat, odborníci na finanční deriváty a portfolia, analýzu rizik, data mining a pojištění. Samozřejmě se tím myslí odborné pozice v centrálách bank, finančních či pojistných institucí, či velkých firem na finančním trhu.

Finanční matematika

Studenti specializace musí ovládat základní postupy a metody finanční matematiky od základního principu úročení až po analýzu typických produktů finančního trhu. V tomto předmětu (a navazujících) se to právě naučí.

Pojistná matematika

Studenti finanční a pojistné matematiky musí znát, jak se dá vypočítat cena pojištění pro různé typy životních i neživotních pojistek, jakým způsobem pojišťovny odhadují své rezervy i jak nastavují bonus/malus systémy. V tomto předmětu se s tím studenti seznámí a vše si ukážou na reálných příkladech.

Data mining

Data mining je osvědčeným způsobem, jakým lze z dat získat maximum informací pro správné rozhodování. Součástí předmětu jsou metody pro odhalování užitečných informací v obsáhlých datových souborech, hledání skupin podobných zákazníků a změn jejich preferencí, analýza úvěrového rizika, detekce podvodů, analýza produktů a mnoho dalšího. Všechno si studenti vyzkouší na cvičeních v nejpoužívanějším komerčním dataminingovém softwaru SAS.

Teorie portfolia

Předmět primárně vyučovaný na ESF MU. Věnuje se základním metodám v oblasti vyhodnocování investičních variant, optimalizace portfolia a oceňování rizikových a nerizikových aktiv, konkrétně Markowitzův model, model oceňování kapitálových aktiv, diverzifikace rizik a arbitrážní teorie oceňování.

Specializace: Statistika a analýza dat

Tato specializace je určena studentům, kteří se chtějí uplatnit v široké oblasti statistické analýzy dat. Nalézt uplatnění je možné v mnoha institucích, od zpracování laboratorních, medicínských či vědeckých dat až po oblast komerční sféry.

Výpočetní statistika

Předmět ukáže jak aplikovat základní statistické metody na datové soubory a získat tak zajímavé informace v nich ukryté. Studenti se naučí ovládat jeden z nejúspěšnějších komerčních softwarových statistických systémů TIBCO Statistica. V kurzu lze navíc využít nabídky získat certifikát, který potvrzuje znalosti tohoto softwaru. To se na trhu práce vždy hodí.

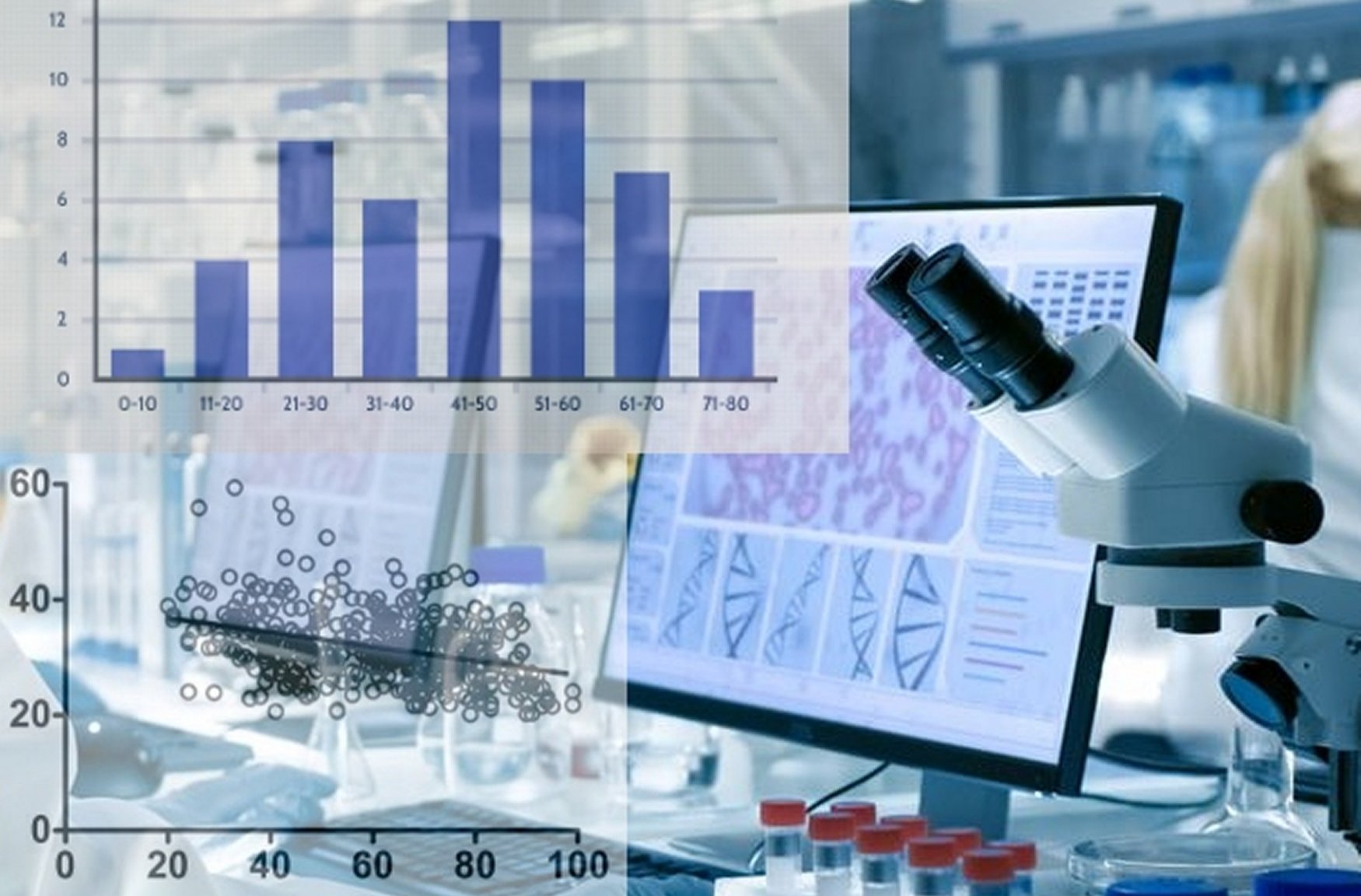
Lineární statistické modely

Předmět dává ucelený pohled na lineární modely jako stěžejní metody statistické analýzy, od teorie po softwarovou implementaci (v programu R). Studenti se naučí rozeznat situace, které lze řešit s pomocí lineárních modelů, formulovat model, implementovat jej a interpretovat jeho výsledky. Stejně tak je potřeba odhadnout jejich limity, případně navrhnout menší modifikací procedury.

Data mining

Data mining je osvědčeným způsobem, jakým lze z dat získat maximum informací pro správné rozhodování. Součástí předmětu jsou metody pro odhalování užitečných informací v obsáhlých datových souborech, hledání skupin podobných zákazníků a změn jejich preferencí, analýza úvěrového rizika, detekce podvodů, analýza produktů a mnoho dalšího. Všechno si studenti vyzkouší na cvičeních v nejpoužívanějším komerčním dataminingovém softwaru SAS.

Specializace: Modelování a výpočty

Tato specializace je určena studentům, kteří se chtějí uplatnit v modelování a simulacích reálných dějů, jak stochastických, tak deterministických. Uplatnění je možné nalézt v širokém spektru oblastí od medicíny, neurovědy, ekologie či epidemiologie až po makroekonomii či matematiku samotnou, jejíž vědecká oblast numerické matematiky se stále rozvíjí.

Algoritmizace úloh a numerické výpočty

Předmět slouží k pochopení, jak využít základní matematické znalostí z lineární algebry v praxi. Studenti se naučí implementovat různé algoritmy s použitím programu Matlab: generovat a zpracovávat data, zobrazovat jejich grafický výstup, využít různé nástroje založené na lineární algebře k vyrovnávání řad, nalezení okrajů nebo rozmazání obrázku, jak modelovat dynamicky se měnící populaci i úlohy s markovskými procesy, řešit soustavy rovnic či optimalizovat metodou nejmenších čtverců.

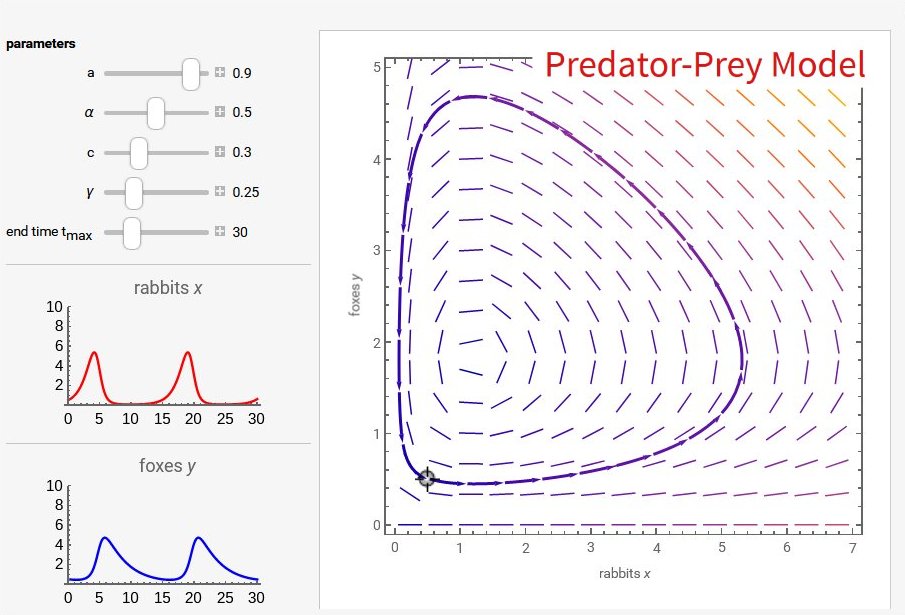
Spojité deterministické modely

Předmět poskytuje základní přehled o teorii obyčejných diferenciálních rovnic. Matematické modelování pomocí těchto rovnic má velkou výhodu, protože jej lze použít v mnoha rozličných oblastech. Student bude schopen použít elementární metody jejich řešení a rozumět jednoduchým spojitým deterministickým modelům v biologii a ekonomii.

Nelineární dynamika a její aplikace

Mnohé složitější dynamické modely lze najít v biochemii, epidemiologii, neurovědě, ekonomii, fyzice, populační biologii nebo v ekologii. Předmět slouží k porozumění obecným nelineárním dynamickým (matematicky generickým) jevům, které v nich vznikají, ale mají také významné aplikace jako jsou biochemické přepínače, vznik oscilací (ať už jde o pískot brzd nebo vzruchy neuronů), zánik populací nebo nepředvídatelné chaotické chování.

Lineární statistické modely

Předmět dává ucelený pohled na lineární modely jako stěžejní metody statistické analýzy, od teorie po softwarovou implementaci (v programu R). Studenti se naučí rozeznat situace, které lze řešit s pomocí lineárních modelů, formulovat model, implementovat jej a interpretovat jeho výsledky. Stejně tak je potřeba odhadnout jejich limity, případně navrhnout menší modifikací procedury.